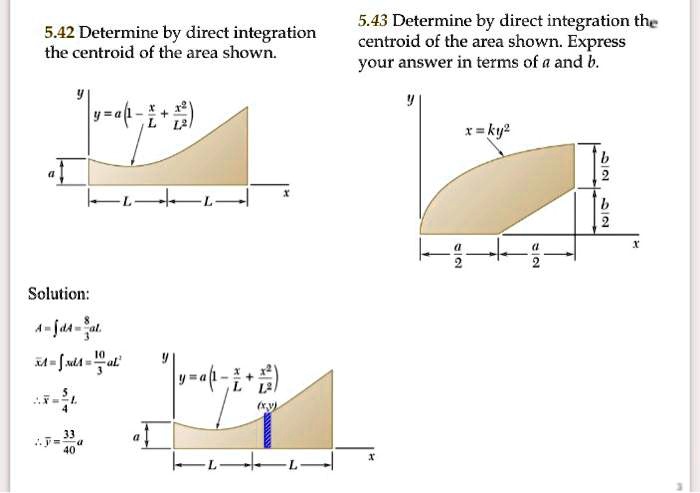
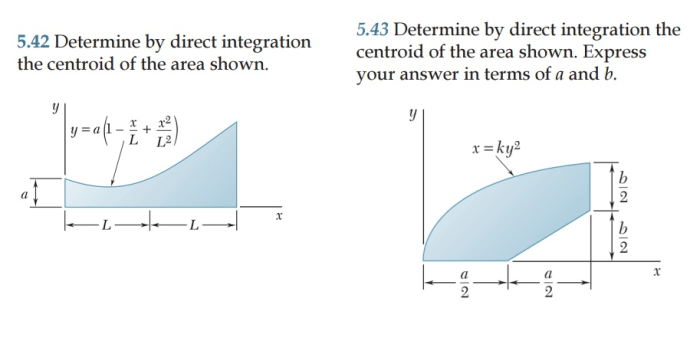
Determine by direct integration the centroid of the area shown – Determining the centroid of an area is a fundamental concept in geometry, providing valuable insights into the center of mass and other physical properties. This article delves into the powerful technique of direct integration to calculate the centroid of intricate areas, offering a comprehensive exploration of its mathematical underpinnings, practical applications, and advanced extensions.
Determine the Centroid of an Area by Direct Integration: Determine By Direct Integration The Centroid Of The Area Shown

In geometry, the centroid of an area represents its geometric center. It is a crucial point that plays a significant role in various applications, such as engineering and physics. Direct integration is a powerful technique used to calculate the centroid of an area with irregular shapes or complex boundaries.
Mathematical Background
The formula for calculating the centroid ( x̄, ȳ) of an area Ausing direct integration is:
x̄= (1/A) ∫∫ Ax dA
ȳ= (1/A) ∫∫ Ay dA
where xand yare the coordinates of a point within the area A.
Step-by-Step Procedure
- Define the Boundaries:Identify the boundaries of the area for which the centroid is to be determined.
- Set up the Integrals:Set up the integrals for x̄and ȳusing the given formula.
- Evaluate the Integrals:Evaluate the integrals to obtain the values of x̄and ȳ.
Examples and Applications
| Shape | Dimensions | Centroid Coordinates (x̄, ȳ) |
|---|---|---|
| Rectangle | Length: a, Width: b | (a/2, b/2) |
| Triangle | Base: b, Height: h | (b/3, h/3) |
| Circle | Radius: r | (0, 0) |
Centroids have practical applications in:
- Structural engineering: Determining the center of gravity of structures for stability and load distribution.
- Physics: Calculating the center of mass of objects for motion and equilibrium analysis.
- Image processing: Locating the center of an object in an image for object recognition and tracking.
Advanced Techniques, Determine by direct integration the centroid of the area shown
- Polar Coordinates:For non-rectangular areas, polar coordinates can be used to simplify the integrals.
- Green’s Theorem:This theorem can be applied to simplify calculations for complex shapes.
- Numerical Integration:Numerical methods can be used to approximate the integrals for complex shapes.
FAQ Resource
What is the significance of determining the centroid of an area?
The centroid serves as the geometric center of an area, representing the point where the entire mass of the area would be concentrated if it were uniformly distributed.
How does direct integration facilitate the calculation of the centroid?
Direct integration involves dividing the area into infinitesimal elements, calculating the coordinates of each element, and then integrating over the entire area to determine the average coordinates, which represent the centroid.